Logarithms

Okey everyone~ Now, I'm going to teach you how to do logarithm. But, before that we must know what is mean by logarithm first!

What is logarithm?

In mathematics, the logarithm is the inverse operation to exponentiation. That means the logarithm of a number is theexponent to which another fixed value, the base, must be raised to produce that number

Introduction to Logarithms

Example: How many 2s do we multiply to get 8?

Answer: 2 × 2 × 2 = 8, so we needed to multiply 3 of the 2s to get 8

So the logarithm is 3

Example 1:

Step 1

We write "the number of 2s we need to multiply to get 8 is 3" as:

log₂(8) = 3

So these two things are the same:

The number we are multiplying is called the "base", so we can say:

• "the logarithm of 8 with base 2 is 3"
• or "log base 2 of 8 is 3"
• or "the base-2 log of 8 is 3"

Notice we are dealing with three numbers:

• the base: the number we are multiplying (a "2" in the example above)
• how many times to use it in a multiplication (3 times, which is the logarithm)
• The number we want to get (an "8")

Example 2

Example: What is log₅(625) ... ?

We are asking "how many 5s need to be multiplied together to get 625?"

5 × 5 × 5 × 5 = 625, so we need 4 of the 5s

Answer: log₅(625) = 4

Example: What is log₂(64) ... ?

We are asking "how many 2s need to be multiplied together to get 64?"

2 × 2 × 2 × 2 × 2 × 2 = 64, so we need 6 of the 2s

Answer: log₂(64) = 6

Exponents

Exponents and Logarithms are related, let's find out how ...

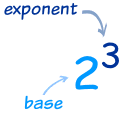The exponent says how many times to use the number in a multiplication. In this example: 23 = 2 × 2 × 2 = 8 (2 is used 3 times in a multiplication to get 8)

So a logarithm answers is like this:

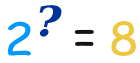
In this way:

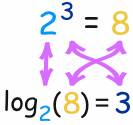
The logarithm tells us what the exponent is!

In that example the "base" is 2 and the "exponent" is 3:

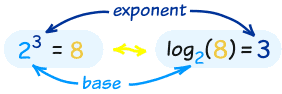
So the logarithm answers the question:

What exponent do we need 
(for one number to become another number) ?

The general case is:

Example: What is log₁₀(100) ... ?

10² = 100

So an exponent of 2 is needed to make 10 into 100, and:

log₁₀(100) = 2

Example: What is log₃(81) ... ?

3⁴ = 81

So an exponent of 4 is needed to make 3 into 81, and:

log₃(81) = 4

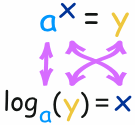
 Another example :

This example is use the law  of logarithm to solve the following :

Example 1 : log_{32 +} log₃₅

 log_{32 +} log₃₅ 

Step 1

Change + into x first!

 log_32 x log₃₅ 

step 2,

Then multiply 2 and 5

log_32x5

So, the answer is log_32x5

= LOg₃₁₀